跟着数码相机、手机等建造成像时间的冉冉教育， 数字图像的取得变得越来越容易， 其在使命和生计中演出着越来越进攻的扮装. 同期， 很多功能强劲且易于操作的图像处理器具使得对图像实质进行修改操作的门槛变低， 非专科的用户也不错玩猝然对图像实质进行修改， 这对数字图像的完好意思性和确切性产生了逼迫[1， 2]. 因此AV解说， 怎样有用识别和认证数字图像成为了亟待处罚的进攻问题[3].

感知图像哈希是图像认证范围中的热门接头问题. 图像哈希是指用一串固定长度的字符或数字序列来示意图像的感知实质， 不错相识为图像视觉实质的压缩抒发， 也称为图像指纹. 图像哈希的生成不会改动图像的实质， 频年来被平素应用于图像认证、数字水印和图像检索等范围. 还是有很多接头东说念主员提议了有用的时间来加快图像哈希的发展， 早期Schneider和Chang等东说念主提议了一种基于图像实质的数字签名算法， 并将该算法应用于图像认证[4]. Liu等东说念主提议了一种基于Radon变换和不变特征的鲁棒图像哈希时势[5]， 并将其用于图像认证. Tang等东说念主提议了一种基于局部熵和DWT的安全图像哈希有野心[6]， 该有野心被应用于图像删改的考据. Qin等东说念主提议了一种使用非均匀采样的图像哈希有野心[7]. 该有野心在鲁棒性和离别性之间达成了令东说念主舒畅的折衷.

与此同期， 云研讨的出现使得用户不错将多半的图像数据和复杂的图像处理运算交给云工作器来处理， 大大镌汰了用户的存储和研讨包袱. 因为多媒体数据中也包含一些阴私实质， 是以这也带来了数据阴私安全的干系问题[8， 9]. 保护阴私的传统时势是对数据进行加密， 然则对数据加密以后便无法为用户提供一些常见的明文数据工作， 举例对多媒体数据的搜索， 研讨和分析[10， 11]. 因此， 加密域中的安全信号处理时间冉冉成为安全外包这一范围的一个进攻接头主义. 频年来， 加密域中的安全信号处理时间还是得到了平素的接头， 并取得了一定的后果. 法国粹者Erkin是安全信号处理接头范围的引导者和前锋， Erkin等东说念主对加密域多媒体数据的信号处理进行了很好的综述[12]. 由于步调不变特征变换(SIFT)描述符被平素应用于图像处理中， Hsu等东说念主开首提议了用于处罚加密域中安全SIFT特征示意和索要的时势[13]. 他们利用Paillier加密算法的同态特点很好地处罚了加密域中的高斯运算和卷积研讨， 然则他们的有野心莫得很好地处罚SIFT中极值点索要的比拟操作问题， 虚耗了庞杂的存储、研讨和通讯老本. 为了进步效能和安全性， Hu等东说念主提议了一种有用且实用的阴私保护研讨外包协议， 不错达成海量加密图像数据上的SIFT特征索要[14]. 该有野心通过当场分割原始图像数据， 遐想适用于安全乘法和比拟的新颖协议以及由两个沉寂的云工作器共同进行特征研讨， 达到了安全性和有用性的条目. 除此除外， 还有一些针对其他特征的阴私保护有野心. Chen等东说念主提议了一种加密域中的多重分形特征索要和示意时势[15]. 该有野心领先使用暗昧序列按块对图像进行加扰， 然后通过利用暗昧序列的局部当场性和稀奇周期性来遐想加密图像的安全多分形特征索要. Xia等东说念主提议了一种安全的LBP特征索要算法[16]， 在有野心中， 通过块改选， 块内改选和保留规定的像素值替换对图像进行加密. Yang等东说念主提议了一种基于类同态加密(SHE)的阴私保护Hahn矩有野心， 并将其定名为PPHM[17]. 该有野心具有较低的复杂度和较高的安全性， 同期在图像重建和图像识别方面均具有精采的性能. Wang等东说念主提议了一种多用户场景下高效阴私保护的基于实质的图像检索有野心[18]， 该有野心利用欧式距离比拟时间对图像特征向量进行相似度排序并复返top-k扫尾. 同期， 遐想的高效密钥改革协议允许每一个检索用户使用本身的私钥生成查询肯求， 并检索不同数据领有者生成的加密图像. Xiang等东说念主提议了一种基于同态加密系统的图像鲁棒可逆水印算法[19]， 该算法达成了在分歧原始图像进行预处理的情况下可平直在加密后的密文图像中镶嵌水印， 并可分别在加密域或明文域索要水印和恢归附始密文图像或原始明文图像， 而且镶嵌的水印对常见的图像处理操作具有一定的鲁棒性.

加密域中安全信号处理时间的发展在保护了数据阴私安全的同期， 也让更多的明文数据工作得以在加密域中达成[20， 21]， 图像认证即是其中AV解说的一种. 出于安全图像认证的需要， 本文提议了一种加密域鲁棒图像哈希算法， 通过应用同态加密这一安全信号处理时间， 达成了加密域图像哈希的生成. 领先由图像通盘者对图像进行预处理和加密并将加密图像传送至云工作器端， 云工作器端对加密图像进行旋转些许特定角度， 以及水平镜像和垂直镜像的操作， 得到包括原始加密图像在内的些许加密版块. 同期引入东说念主眼视觉特点(human visual system， HVS)， 将加密图像分块后分别研讨图像DCT统共矩阵的变型， 将其与Watson权重矩阵和密钥遗弃的伪当场矩阵进行加密域哈希生成运算， 并将研讨扫尾传送至经受者端. 经受者对加密处理扫尾解密得到明文域处理扫尾， 并进行量化判决以产生固定长度的图像哈希. 凭据本文所提议的加密域哈希算法， 不错进行图像认证的应用， 比拟待认证图像的哈希值与原始图像哈希值， 若它们之间的归一化汉明距离小于事先设定的阈值， 则通过认证， 反之拒却. 本文使命的主要革命点如下: (1)提议了一种基于Paillier同态加密的鲁棒图像哈希算法， 在保护图像阴私安全的同期， 可用于对加密图像的图像认证; (2)引入HVS， 在加密域中通过DCT统共矩阵变型与Watson权重矩阵和伪当场矩阵的密文运算， 达成具有东说念主眼视觉特点的密文哈希生成; (3)本文算法生成的图像哈希对一般的图像实质保合手操作具有鲁棒性， 同期还具有较好的惟一性和安全性.

1 加密域鲁棒图像哈希算法

本文提议的加密域鲁棒图像哈希算法经过图如图1所示. 该系统主要由图像通盘者、云工作器、经受者3部分构成.

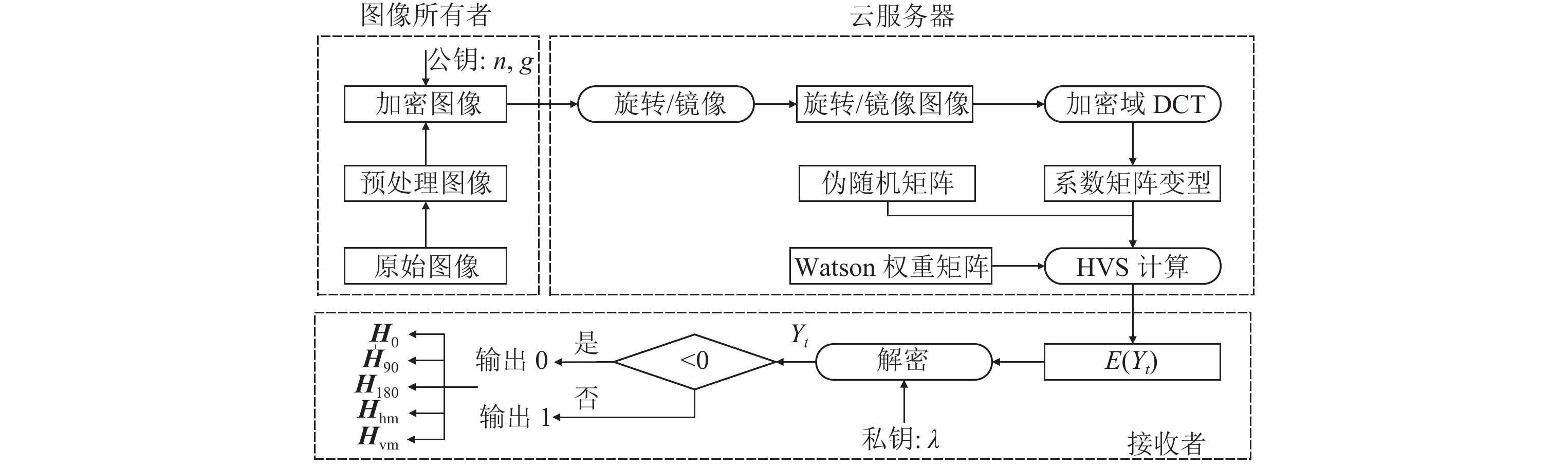Fig. 1 Image feature extraction and hash construction in encrypted domain 图 1 加密域图像特征索要及哈希构造 1.1 预处理和图像加密

利用公式(1)将输入的RGB彩色图像I0改革为灰度图像(若图像还是是灰度， 则不实践此要领)， 然后将灰度图像诊疗至M ×M像素的固定尺寸:

$ {\boldsymbol{I}_1} = 0.2989R + 0.5870G + 0.1140B $ (1)

为了保护图像实质阴私， 对预处理后得到的图像I1使用Paillier同态加密算法进行加密. Paillier密码系统是一种部分同态、非对称的加密有野心. 领先需要生成公钥n， g和私钥λ. 录取两个大素数p和q， 使其知足ψ (pq， (p−1)(q−1)) = 1， ψ(·)代表最大协议数运算符， 不错得到:

$ n = p \times q $ (2) $ \lambda = \varphi \left( {\left( {p - 1} \right)， \left( {q - 1} \right)} \right) $ (3)

其中， φ(·)示意最小公倍数运算符. 选拔g ∈ $ Z_{{n^2}}^* $ ( $ Z_{{n^2}}^{} $ ={0， 1， …， n2−1}， $ Z_{{n^2}}^* $ ∈ $ Z_{{n^2}}^{} $ )， 何况知足:

$ \psi \left( {L\left( {{g^\lambda }\bmod {n^2}} \right)， n} \right) = 1 $ (4)

其中， L(·)界说为L(x) = (x−1)/n， x ∈ N*. 由此不错得到公钥n， g和私钥λ. 对明文m (m ∈ Zn且m < n)欺诈公钥n和g进行加密得到密文c， 见公式(5):

在线影视 $ c = E(m) = {g^m} \times {r^n}\bmod {n^2} $ (5)

其中， E(·)示意Paillier加密函数， r为当场整数且r ∈ $ Z_{{n^2}}^* $ . 当场数r保证了Paillier加密的非细目性， 即关于销亡个明文m， 由于r的不同， 其得到的对应密文c可能不同. Paillier解密操作的要领如下: 关于密文c， 不错凭据公式(6)回复得到原始明文m:

$ m = D(c) = \left( {L({c^\lambda }\bmod {n^2}) \times \mu } \right)\bmod n $ (6)

其中， D(·)示意Paillier解密函数， μ = [L(gλ mod n2)]−1 mod n. 因此， 凭据公式(5)， 可对图像I1进行Paillier加密操作得到密文图像I:

$ {I}(x， y) = E\left( {{\boldsymbol{I}_1}(x， y)} \right) = ({g^{{{I}_1}(x， y)}} \times {r^n})\bmod {n^2} $ (7)

图像通盘者在对预处理图像进行加密操作之后， 将加密后的图像I发送至云工作器端以进行加密域的图像哈希研讨.

1.2 加密域图像哈希研讨

云工作器经受到来自图像通盘者发送的加密图像后， 领先对加密图像I分别进行固定角度(90°， 180°， 270°)的旋转以及水平镜像和垂直镜像操作， 得到一组加密图像， 包括原始加密图像和旋转、镜像加密图像， 接着在加密域中进行DCT研讨， 得到DCT统共矩阵的变型， 团结Watson权重矩阵以及密钥遗弃的伪当场矩阵研讨得到加密域图像处理扫尾E(Yt)， 并将其传送至经受者端， 由经受者对其进行解密， 并对解密扫尾进行量化判决后， 得到图像哈希值.

1.2.1 加密域图像旋转镜像操作

为了使生成的图像哈希对固定角度旋转以及镜像操作具有一定的鲁棒性， 在特征索要前， 云工作器对加密图像I进行固定角度(90°， 180°， 270°)的旋转以及水平镜像和垂直镜像操作， 不错得到加密图像I的5个不同版块的加密图像. 设P0 (x0，y0)为原始图像中的某个像素点， P1 (x1，y1)为P0 (x0，y0)旋转或镜像操作后得到的图像中对应的像素点. 从原始图像中的P0 (x0，y0)映射到旋转/镜像图像中的P1 (x1，y1)， 其坐标变换如公式(8)所示:

$ \left\{ {\begin{array}{l}{x}_{1}={y}_{0}， {y}_{1}=-{x}_{0}， \;\text{if}\;旋转{90}^{\circ } \\ {x}_{1}=-{x}_{0}+M\text{， }{y}_{1}=-{y}_{0}， \;\text{if}\;旋转{180}^{\circ }\\ {x}_{1}={y}_{0}+M， {y}_{1}=-{x}_{0}+M， \;\text{if}\;旋转{270}^{\circ }\\ {x}_{1}=-{x}_{0}， {y}_{1}={y}_{0}， \;\text{if}\;水平镜像\\ {x}_{1}={x}_{0}， {y}_{1}=-{y}_{0}， \;\text{if}\;垂直镜像 \end{array}} \right. $ (8)

接下来， 云工作器对加密图像I偏执5个旋转镜像版块进行特征索要操作. 下一节将以对加密图像I进行特征索要为例进行文牍.

1.2.2 加密域DCT统共特征索要

领先， 云工作器将加密图像I分红(M/8) × (M/8)个大小为8 × 8的图像块Bi， i = 1， 2， …， M2/64. 再分别对每个图像块Bi进行加密域DCT的研讨. 已知明文域中DCT统共矩阵的研讨如公式(9)所示:

$ F(u， v) = a(u)a(v)\sum\limits_{j = 0}^7 {\sum\limits_{k = 0}^7 {f(j， k) \times \cos \left( {\frac{{(2j + 1)u{\text{π }}}}{{16}}} \right) \times \cos \left( {\frac{{(2k + 1)v{\text{π }}}}{{16}}} \right)} } $ (9)

其中， 当u， v = 0时， a(u)， a(v)= $ \sqrt {1/8} $ ; 当u， v = 1， 2， …， 7时， a(u)， a(v) = $ \sqrt {1/4} $ . 为在索要特征时不受平均亮度影响， 咱们将统共矩阵中的直流统共置零.

由公式(9)可知， a(u)、a(v)、 $ \cos \left( {\dfrac{{(2j + 1)u{\text{π }}}}{{16}}} \right) $ 和 $ \cos \left( {\dfrac{{(2k + 1)v{\text{π }}}}{{16}}} \right) $ 均不是整数. 要是要在加密域中求取DCT统共矩阵， 凭据第1.1节中m ∈ Zn且m < n的条目， 需要先将这几项量化为整数后再进走运算， 即凭据公式(10)进行DCT统共矩阵变型的研讨:

$ F(u， v) = \left[ {{\xi _1}a(u)a(v)} \right] \times \sum\limits_{j = 0}^7 {\sum\limits_{k = 0}^7 {f(j， k) \times \left[ {{\xi _2}\cos \left( {\frac{{(2j + 1)u{\text{π }}}}{{16}}} \right)} \right] \times \left[ {{\xi _2}\cos \left( {\frac{{(2k + 1)v{\text{π }}}}{{16}}} \right)} \right]} } $ (10)

其中， ξ1、ξ2为正整数， 分别示意对a(u)a(v)和 $ \cos \left( {\dfrac{{(2j + 1)u{\text{π }}}}{{16}}} \right) $ 、 $ \cos \left( {\dfrac{{(2k + 1)v{\text{π }}}}{{16}}} \right) $ 的放大倍数， [·]函数示意四舍五入取整运算.

由于公式(10)中的运算为加法和数乘运算， 因此不错利用Paillier密码系统的加法和标量乘法特点进行加密域中的研讨. 凭据同态特点可知， 在合适的模运算下， 对两个密文的乘积进行解密不错得到对应两个明文的和， 对密文的整数指数幂进行解密不错得到该整数指数与对应明文的乘积. 它的同态性质可由公式(11)、公式(12)示意， 其中ξ为整数， 关于两个明文m1和m2， 有:

$ D\left( {\left( {E({m_1}) \times E({m_2})} \right)\bmod {n^2}} \right) = ({m_1} + {m_2})\bmod n $ (11) $ D\left( {E{{({m_1})}^\xi }\bmod {n^2}} \right) = ({m_1} \times \xi )\bmod n $ (12)

由此， 不错得到DCT统共矩阵变型的研讨公式， 如公式(13)所示:

$ \begin{aligned}[b] E\left( {{{\boldsymbol{C}}_i}(u， v)} \right) &= E\left( {\left[ {{\xi _1}a(u)a(v)} \right] \times \sum\limits_{j = 0}^7 {\sum\limits_{k = 0}^7 {{{B}_i}(j， k) \times \left[ {{\xi _2}\cos \left( {\frac{{(2j + 1)u\pi }}{{16}}} \right)} \right] \times \left[ {{\xi _2}\cos \left( {\frac{{(2k + 1)v\pi }}{{16}}} \right)} \right]} } } \right) \\ & = \prod\limits_{j = 0}^7 {\prod\limits_{k = 0}^7 {E\left( {{{B}_i}(j， k) \times \left[ {{\xi _1}a(u)a(v)} \right] \times \left[ {{\xi _2}\cos \left( {\frac{{(2j + 1)u\pi }}{{16}}} \right)} \right] \times \left[ {{\xi _2}\cos \left( {\frac{{(2k + 1)v\pi }}{{16}}} \right)} \right]} \right)} } \bmod {n^2} \\ & = \prod\limits_{j = 0}^7 {\prod\limits_{k = 0}^7 {E{{\left( {{{B}_i}(j， k)} \right)}^{\left[ {{\xi _1}a(u)a(v)} \right] \times \left[ {{\xi _2}\cos \left( {\frac{{(2j + 1)u\pi }}{{16}}} \right)} \right] \times \left[ {{\xi _2}\cos \left( {\frac{{(2k + 1)v\pi }}{{16}}} \right)} \right]}}} } \bmod {n^2} \end{aligned} $ (13)

其中， Ci为图像块的统共矩阵的变型， 大小为8 × 8. 由公式(13)得到每个图像块的统共矩阵的变型后， 再将其按图像块在原图像中的位置拼接得到图像的DCT统共矩阵的变型C， 大小为M ×M. 需要泄露的是， 在研讨中， 把ξ1a(u)a(v)、ξ2 $ \cos \left( {\dfrac{{(2j + 1)u{\text{π }}}}{{16}}} \right) $ 和ξ2 $ \cos \left( {\dfrac{{(2k + 1)v{\text{π }}}}{{16}}} \right) $ 动作全体来进行研讨以减少加密域中的指数运算次数， 从而进步研讨效能.

1.2.3 基于HVS的密文哈希研讨

云工作器研讨得到图像统共矩阵变型后， 团结由密钥遗弃的伪当场矩阵以及Watson视觉模子， 进行基于HVS的密文哈希研讨.

领先， 为了进步生成哈希的安全性， 凭据密钥K生成τ个与C大小相通的伪当场矩阵Dt， t = 1， 2， …， τ. 矩阵中元素相互沉寂， 且征服模范正态漫步. 将Dt进行取整处理得到[ξ3Dt]， 并凭据公式(5)将其加密， 研讨公式如公式(14)所示:

$ E(\left[ {{\xi _3}{{D}_t}} \right]) = ({g^{\left[ {{\xi _3}{{D}_t}} \right]}} \times {r^n})\bmod {n^2} $ (14)

其中， ξ3为正整数. 莫得密钥K的情况下， 无法得到十足相通的伪当场矩阵， 具有一定的安全性.

基于Watson东说念主眼视觉模子引入DCT频率明锐度矩阵A， 矩阵中的每个元素的值示意图像分块在莫得装潢噪声的情况下， 对应位置的DCT统共可被察觉的最小修改幅度， 这个值越小， 泄露东说念主眼对该频率越明锐， 也即是说该频率统共对图像视觉实质越进攻， 其在频率特征值中占的比例应该越大， 因而在研讨特征值时可将矩阵A中的每个元素的倒数动作对应位置DCT频率的权重. 周期延拓矩阵A， 并将延拓后矩阵中的元素取倒数， 得到大小为M × M的Watson权重矩阵Q， A和Q如公式(15)所示. 相似的， 由于Q中元素不是整数， 需要将其化为整数后再进行研讨， 对Watson权重矩阵Q进行取整操作[ξ4Q]， ξ4为正整数.

$\begin{aligned} {\boldsymbol{A}} = \left(\begin{array}{*{20}{c}} {1.40}&{1.01}&{1.16}&{1.66}&{2.40}&{3.43}&{4.79}&{6.56} \\ {1.01}&{1.45}&{1.32}&{1.52}&{2.00}&{2.71}&{3.67}&{4.93} \\ {1.16}&{1.32}&{2.24}&{2.59}&{2.98}&{3.64}&{4.60}&{5.88} \\ {1.66}&{1.52}&{2.59}&{3.77}&{4.55}&{5.30}&{6.28}&{7.60} \\ {2.40}&{2.20}&{2.98}&{4.55}&{6.15}&{7.46}&{8.71}&{10.17} \\ {3.43}&{2.71}&{3.64}&{5.30}&{7.46}&{9.62}&{11.58}&{13.51} \\ {4.79}&{3.67}&{4.60}&{6.28}&{8.71}&{11.58}&{14.50}&{17.29} \\ {6.56}&{4.93}&{5.88}&{7.60}&{10.17}&{13.51}&{17.29}&{21.15} \end{array}\right)，\\ Q = \left(\begin{array}{ccc:c:ccc} {0.7143} & \cdots &{0.1524} & {} & {0.7143} & \cdots & {0.1524} \\ \vdots & \ddots & \vdots & \cdots & \vdots & \ddots & \vdots \\ {0.1524} & \cdots & {0.0473} & {}& {0.1524} & \cdots & {0.0473} \\ \hdashline {} & \vdots & {} & \ddots & {} & \vdots &{} \\ \hdashline \\ {0.7143} & \cdots & {0.1524} & {} & {0.7143} & \cdots &{0.1524} \\ \vdots & \ddots & \vdots & \cdots & \vdots & \ddots & \vdots \\ {0.1524} & \cdots & {0.0473} & {} & {0.1524} & \cdots & {0.0473}\end{array}\right)\end{aligned}$ (15)

云工作器利用Watson权重矩阵Q增大东说念主眼明锐的频率统共在研讨图像哈希时所占比重， 并利用伪当场矩阵加多哈希的安全性， 研讨得到基于HVS的密文哈希研讨扫尾. 研讨公式如公式(16)所示， 其中， t = 1， 2，…， τ.

$ \begin{aligned}[b] E({Y_t}) &= E\left( {\sum\limits_{p = 1}^M {\sum\limits_{q = 1}^M {C(p， q) \times \left[ {{\xi _3}{D_t}(p， q)} \right] \times \left[ {{\xi _4}{Q}(p， q)} \right]} } } \right) \\ & = \prod\limits_{p = 1}^M {\prod\limits_{q = 1}^M {E\left( {{C}(p， q) \times \left[ {{\xi _3}{D_t}(p， q)} \right] \times \left[ {{\xi _4}{Q}(p， q)} \right]} \right)} } \bmod {n^2} \\ & = \prod\limits_{p = 1}^M {\prod\limits_{q = 1}^M {E{{\left( {{C}(p， q)} \right)}^{\left[ {{\xi _3}{D_t}(p， q)} \right] \times \left[ {{\xi _4}{Q}(p， q)} \right]}}} } \bmod {n^2} \end{aligned} $ (16)

至此， 云工作器得到加密域的密文哈希研讨扫尾E(Yt)， 则密文哈希不错示意为: E(H0) = [E(Y1)， E(Y2)，…， E(Yτ)]， 将其解密便不错得到图像的明文哈希值. 基于HVS的图像哈希算法好像反馈东说念主眼的视觉特点， 增大对东说念主眼明锐的频域统共(即图像主要实质特征)在研讨图像哈希时的权重.

1.3 解密和明文哈希生成

经受者从云工作器端经受到加密域研讨扫尾E(Yt)后， 对其进行解密操作. 经受者利用私钥λ并团结公式(6)对E(Yt)进行解密， 得到Yt的值， 如公式(17)所示.

$ {Y_t} = D\left( {E({Y_t})} \right) = \left( {L\left( {E{{({Y_t})}^\lambda }\bmod {n^2}} \right) \times \mu } \right)\bmod n $ (17)

将Yt与0进行大小比拟AV解说， 若Yt大于等于0， 则ht为1， 不然， ht为0， 其中t = 1， 2，…， τ， 不错得到原始图像的哈希值H0 = [h1， h2， …， hτ]. 同理， 关于旋转加密图像和镜像加密图像， 可得到旋转图像哈希值H90， H180， H270以及镜像图像哈希值Hhm， Hvm. 完好意思的图像哈希值示意为H = {H0